Probability Sensitivity Analysis (PSA)

Introduction

PSA is a core part of any cost-effectiveness analysis (Briggs et al. 2012). Here we will carry this out for a simple decision tree. This involves repeatedly sampling from a distribution for each branch probability and cost and calculating the total expected value for each set of realisations.

Example

library(CEdecisiontree, quietly = TRUE)
library(assertthat, quietly = TRUE)
library(treeSimR, quietly = TRUE)
library(tibble, quietly = TRUE)
library(tidyverse, quietly = TRUE)
library(purrr, quietly = TRUE)

We first define the decision tree. The difference to previous trees is that we now use the list-column feature to define distributions rather than point values.

tree_dat <-
  list(child = list("1" = c(2, 3),
                    "2" = NULL,
                    "3" = NULL),
       dat = tibble(
         node = 1:3,
         prob =
           list(
             NA_real_,
             list(distn = "unif", params = c(min = 0, max = 1)),
             list(distn = "unif", params = c(min = 0, max = 1))),
         vals =
           list(
             0L,
             list(distn = "unif", params = c(min = 0, max = 1)),
             list(distn = "unif", params = c(min = 0, max = 1)))))

tree_dat
#> $child
#> $child$`1`
#> [1] 2 3
#> 
#> $child$`2`
#> NULL
#> 
#> $child$`3`
#> NULL
#> 
#> 
#> $dat
#> # A tibble: 3 × 3
#>    node prob             vals            
#>   <int> <list>           <list>          
#> 1     1 <dbl [1]>        <int [1]>       
#> 2     2 <named list [2]> <named list [2]>
#> 3     3 <named list [2]> <named list [2]>

We can now loop over this tree and generate samples of values for the given distributions. We use the sample_distributions() function from my treeSimR package. This is all wrapped up in the convenience function create_psa_inputs.

library(purrr)

tree_dat_sa <- create_psa_inputs(tree_dat, n = 1000)

This results in a list of trees.

head(tree_dat_sa, 2)
#> [[1]]
#> $child
#> $child$`1`
#> [1] 2 3
#> 
#> $child$`2`
#> NULL
#> 
#> $child$`3`
#> NULL
#> 
#> 
#> $dat
#>   node      prob      vals
#> 1    1        NA 0.0000000
#> 2    2 0.9626497 0.2399404
#> 3    3 0.5228080 0.3990208
#> 
#> attr(,"class")
#> [1] "tree_dat" "list"    
#> 
#> [[2]]
#> $child
#> $child$`1`
#> [1] 2 3
#> 
#> $child$`2`
#> NULL
#> 
#> $child$`3`
#> NULL
#> 
#> 
#> $dat
#>   node       prob       vals
#> 1    1         NA 0.00000000
#> 2    2 0.91564742 0.47827629
#> 3    3 0.03897943 0.02314612
#> 
#> attr(,"class")
#> [1] "tree_dat" "list"

Now it is straightforward to map over each of these trees to obtain the total expected values

res <- map_dbl(tree_dat_sa, dectree_expected_values)
head(res)
#> [1] 0.4395898 0.4388347 0.9441533 0.6099253 0.5126502 0.4441804


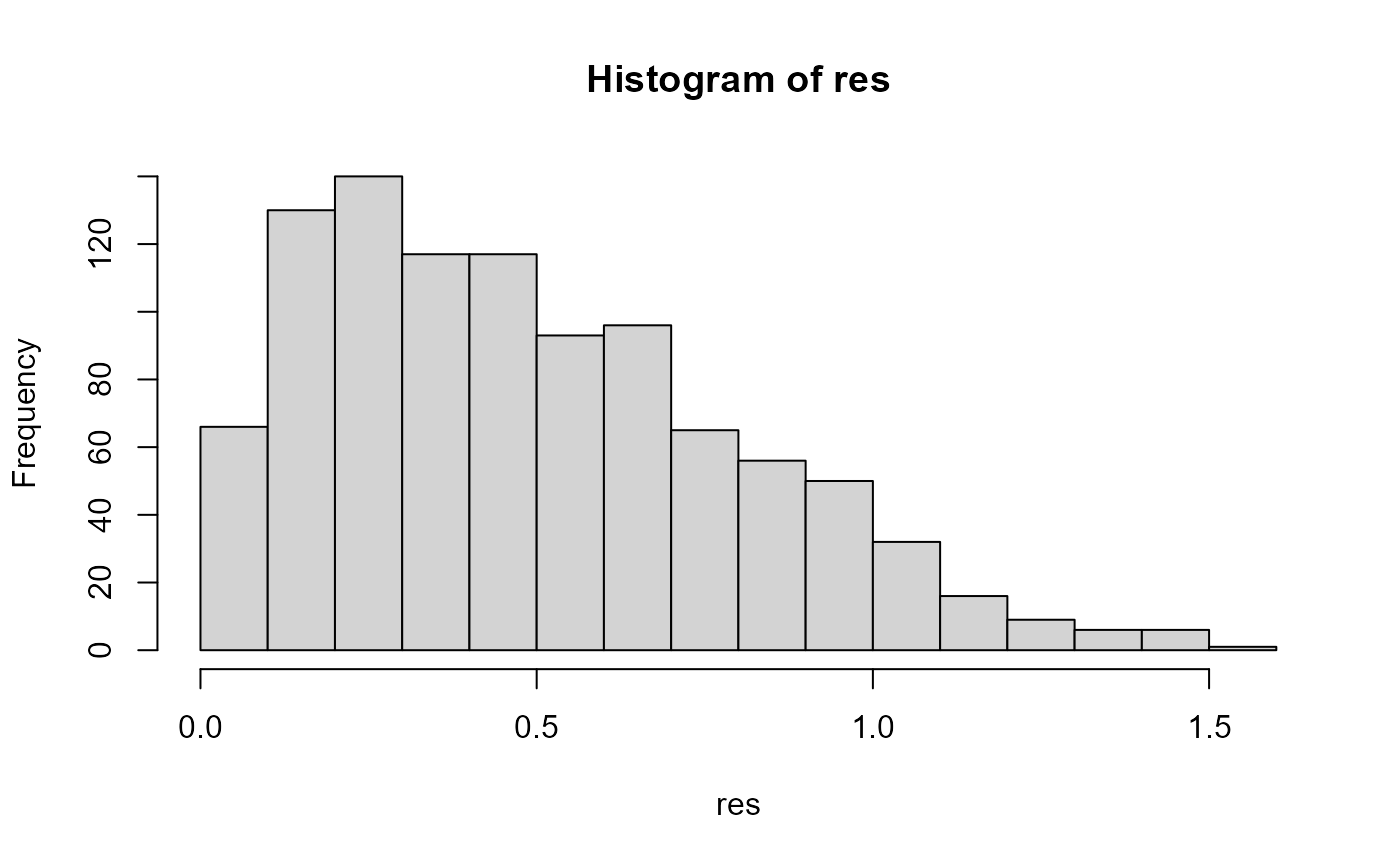
hist(res, breaks = 20)

References

Briggs, Andrew H, Milton C Weinstein, Elisabeth AL Fenwick, Jonathan Karnon, Mark J Sculpher, and A David Paltiel. 2012. “Model Parameter Estimation and Uncertainty: A Report of the ISPOR-SMDM Modeling Good Research Practices Task Force-6 on Behalf of the ISPOR-SMDM Modeling Good Research Practices Task Force Background to the Task Force.” Value in Health 15 15: 835–42. https://doi.org/10.1016/j.jval.2012.04.014.

Nathan Green

2022-08-17

Introduction

Example

References